25 astuces simples de maths mentale qui vont souffler votre esprit

Pour voir si un nombre est divisible par trois, additionnez les chiffres. Si la somme est divisible par trois, il en est de même pour le nombre. Note: cela fonctionne aussi pour 9.

x% de y est identique à y% de x. Cela signifie que si 2% de 50 est trop difficile à comprendre, vous pouvez simplement le retourner - 50% de 2. C'est beaucoup plus facile.

Pour multiplier un nombre à 2 chiffres par 11, il suffit d'ajouter les chiffres ensemble et de coller la réponse entre eux. Par exemple 42 * 11 serait 4 + 2 = 6. Maintenant, mettez le 6 entre le 4 et le 2 pour obtenir 462.

Note: N'oubliez pas de porter le 1. Pour donner un autre exemple, 58 * 11 serait 5 + 8 = 13. Vous ne pouvez pas simplement mettre le 13 entre le 5 et le 8 bien. Cela donnerait 5138, ce qui est évidemment faux. Vous devez porter l'un en l'ajoutant au 5. Donc ce serait 638.

Si vous devez multiplier un nombre par 5, il peut être plus facile de le réduire de moitié et de le multiplier par 10. Par exemple, 315 * 5 serait 315/2 = 157.5 Maintenant, déplacez la décimale pour multiplier par 10 et obtenez 1575.

Pour approximer une racine carrée, procédez comme suit. Trouvez le prochain carré parfait inférieur. Ajoutez-le à votre numéro. Maintenant, divisez par la racine carrée du carré parfait inférieur. Et divisez maintenant par 2. Cela semble dur? Voici un exemple. Prenez 31. Le prochain carré parfait le plus bas est 25. Donc 31 plus 25 est 56. Maintenant, divisez par la racine carrée de 25. Donc 56/5 = 11.2 Maintenant, divisez par 2 pour obtenir 5.6

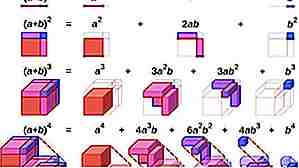
Utilisez le théorème binomial (a + b) ^ 2 = a ^ 2 + 2ab + b ^ 2 pour les nombres carrés. Par exemple 55 ^ 2 pourrait être (50 + 5) ^ 2. Cela signifie que 50 * 50 + 50 * 5 * 2 + 5 * 5 = 2500 + 500 + 25 = 3025.

Pour voir si un nombre est divisible par 8, vérifiez les trois derniers chiffres. Si elles sont divisibles par 8, alors le nombre est divisible par 8. Par exemple, 3423024 serait divisible par 8 parce que 024/8 = 3

Pour comprendre une astuce, il suffit de déplacer la décimale d'une place vers la gauche pour obtenir 10%. Ensuite, soit ajouter la moitié de ce qu'il vous reste pour obtenir 15% ou le doubler pour 20%. Par exemple, si la facture est de 43, 21 $, alors 4, 32 $ est de 10%. La moitié de 4, 32 $ est 2, 16 $, donc si vous voulez 15%, ajoutez-le. Il vous donnerait 4, 32 $ + 2, 16 $ = 6, 48 $. Obtenir 20% est encore plus facile parce que vous venez de le doubler. 4, 32 $ * 2 = 8, 64 $. Donc, si vous vous sentez généreux alors 8, 64 $ constituerait un pourboire de 20%.

Pour calculer votre salaire annuel, prenez votre salaire horaire, doublez-le et ajoutez 3 zéros. Disons que vous faites 8 $ par heure. Juste le double pour 16 $ et ajoutez trois zéros pour 16 000 $.

Pour approximer les conversions entre Celsius et Fahrenheit, il suffit de multiplier par 2 et d'ajouter 30 (de C à F). Faites l'inverse pour aller de F à C (soustraire 30 et diviser par 2).

Pour voir si un nombre est divisible par 4 il suffit de regarder les deux derniers chiffres. Si elles sont divisibles par 4 alors le nombre est divisible par 4. Donc 23746316 serait divisible par 4 car 16 est divisible par 4.

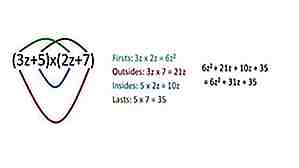
Pour multiplier deux nombres ensemble, utilisez la méthode FOIL (first, outer, inner, last). Par exemple, 25 * 37 serait (20) (30) + (5) (30) + (7) (20) + (5) (7) = 925.

Note: c'est exactement ce que vous faites lorsque vous multipliez sur papier, il est simplement plus facile de visualiser la méthode FOIL dans votre tête.

Pour calculer le pourcentage d'un nombre (ce qui n'est pas 10%), trouvez d'abord 1%, puis multipliez-le. Ainsi, par exemple, 3% de 528 serait 528 * .01 = 5.28 (déplacez les deux décimales restantes). Maintenant il suffit de multiplier par 3 pour obtenir 15.84

Cela fonctionne particulièrement bien si l'un des nombres est déjà gentil et rond (se termine par 0). Arrondissez simplement l'autre nombre, multipliez et ajustez le résultat en conséquence. Par exemple, si vous voulez calculer 18 * 30 vous n'avez pas besoin de la méthode FOIL que nous avons fait plus tôt (parce que 30 est déjà sympa et rond). Il suffit de faire 20 * 30 qui est de 600 et ensuite soustraire deux 30s pour 540.

Pour vérifier si un nombre est divisible par 6, vous devez combiner deux règles de divisibilité (deux et trois). Si elle est divisible par 2 et 3, alors elle est divisible par 6. Nous avons déjà divisibilisé par 3, mais juste au cas où ... les nombres pairs sont divisibles par 2.

La représentation décimale des 11 peut être faite en multipliant le numérateur par 9 et en le répétant simplement. Par exemple, 1/11 = .09090909 .... et 2/11 = .18181818 ... etc

Pour mettre en carré n'importe quel nombre à deux chiffres qui se termine par 5, mettez simplement 25 à la fin et multipliez le premier chiffre par le chiffre suivant. Donc, par exemple, 45 ^ 2 serait 2025 parce que 5 est le prochain chiffre au-dessus de 4, donc 4 * 5 = 20. Maintenant, mettez juste un 25 sur la fin pour 2025.

Les représentations décimales pour les neuvièmes ne sont que le numérateur répété. Par exemple 1/9 = .1111111 ... et 2/9 = .2222222 ... C'est aussi l'une des preuves utilisées pour montrer que .999999 ... = 1. (depuis 9/9 = .99999 ...)

Pour les nombres au carré, une astuce possible consiste à ajouter / soustraire du nombre jusqu'à ce que vous obteniez deux nombres que vous pouvez facilement multiplier. Ensuite, ajoutez la différence du nombre que vous avez ajouté / soustrait. Pour donner un exemple, 46 ^ 2 pourrait être 42 * 50 parce que 46 - 4 = 42 et 46 + 4 = 50. Donc 42 * 50 serait 2100. Maintenant placez le nombre que vous avez ajouté / soustrait donc 4 ^ 2 = 16. Maintenant ajouter 16 pour obtenir 2116.

72 divisé par le taux d'intérêt vous donnera une estimation approximative du nombre d'années qu'il faudrait pour doubler votre argent (règle de 72).

Pour faire un ajout mental, il est beaucoup plus facile de travailler de gauche à droite plutôt que sur papier (de droite à gauche). C'est parce que votre cerveau reconnaît naturellement et se souvient des nombres commençant à gauche. Par exemple, pour faire 376 + 581, ajouter 300 + 500 pour obtenir 800. Maintenant, ajoutez 70 + 80, ce qui est 150. Cela porte le total à 950. Puis ajoutez le 7 pour obtenir 957. Fondamentalement, casser l'addition vers le bas en plus petites parties de gauche à droite. Un autre avantage de ceci est que vous allez progressivement intégrer la solution. Donc, si vous voulez seulement une approximation, vous n'avez pas à attendre jusqu'à ce que vous ayez fini le problème pour déterminer l'ordre de grandeur avec lequel vous travaillez (des centaines, des milliers, etc.)

Pour la soustraction mentale, l'idée est similaire à l'addition. Travaillez de gauche à droite, mais il y a une astuce supplémentaire que vous devez connaître (indice: il s'agit d'arrondir). Disons que vous voulez faire 632 - 487. Tout d'abord, ajoutez 3 pour arrondir 487 jusqu'au 10 le plus proche, donc 490. Maintenant, le problème devient 632 - 490. C'est beaucoup plus facile. 632 - 400 est 232. Maintenant, en soustrayant 90 vous obtenez 142 (c'est 10 de plus que soustraire 100). De là, n'oubliez pas de rajouter le 3 depuis le début. Cela vous donne 145.

Une autre astuce pour multiplier les nombres qui sont facilement arrondis (se terminant généralement par 8 ou 9) est d'utiliser la méthode de soustraction. Pour ce faire, vous arrondissez le nombre puis soustrayez. Par exemple, 49 * 16 serait 50 * 16. C'est beaucoup plus facile à résoudre. Puisque 100 * 16 est 1600, vous pouvez réduire la moitié de cela à 800. Maintenant, n'oubliez pas de soustraire ce que vous avez arrondi au début. Donc, puisque vous avez arrondi 49 à 50, c'était 1 * 16, ce que vous devez soustraire. Cela donne 800 - 16 qui est 784.

Rappelez-vous que vous pouvez faire tout ce que vous voulez pour une équation aussi longtemps que vous le faites des deux côtés. En outre, vous pouvez faire ce que vous voulez pour un terme, tant que vous le multipliez par un. Gardez à l'esprit que 1 a des formes infinies (2/2, (x-4) / (x-4), etc.).

Pour convertir des miles en kilomètres, vous pouvez obtenir une estimation assez proche en ajoutant 60%. Le moyen le plus rapide de le faire est d'ajouter 50% puis 10%. Par exemple. 60 milles en km seraient les suivants: 60 * .5 = 30 et 60 * .1 = 6. Maintenant, 30 + 6 = 36. Ajoutez ceci à 60 pour obtenir 96 km. Pour aller de kilomètres en miles, il suffit de soustraire 40%. Vous pouvez le faire en soustrayant 50%, puis en ajoutant 10%. Donc, pour obtenir 350 km en miles, soustrayez la moitié de 350. Cela vous donne 175. Maintenant, rajoutez 10% de 350 qui est 35. Cela vous laisse avec 210. Remarque: gardez à l'esprit que ce sont des estimations très approximatives. Plus vos chiffres sont importants, plus il y aura d'erreurs.