Les maths sont fous. Alors que les bases sont assez simples, la philosophie derrière certains de ces fondamentaux très simples peut être assez profonde ... et même déconcertante. Aujourd'hui, nous allons regarder tout des nombres premiers à l'infini. Alors préparez-vous parce que ce sont 25 principes mathématiques extraordinaires pour défier votre cerveau!
La corde de l'équateur
 Source: abc.net.au, Image: pexels (domaine public)
Source: abc.net.au, Image: pexels (domaine public) Si vous enrouliez une corde autour de l'équateur de la Terre afin qu'elle soit étroitement serrée au sol, il vous suffirait d'ajouter environ 6, 3 mètres de corde pour que l'ensemble de la surface plane à 1 mètre du sol (tout autour du Terre). Ce résultat contre-intuitif fonctionne quelle que soit la taille de la sphère. La manière la plus simple d'expliquer ceci est de se rappeler que la circonférence est égale au diamètre multiplié par pi. Cela signifie que si vous voulez faire planer la corde à 1 mètre au-dessus de la Terre, il vous suffit d'augmenter le diamètre de 2 mètres (1 mètre à chaque extrémité du globe). Par conséquent, vous auriez seulement besoin d'augmenter la circonférence de la corde de 2 x pi mètres (6.28318530718 mètres).
Hippasus de Metapontum
 Source: esoterx.com, Image: https://commons.wikimedia.org (domaine public)
Source: esoterx.com, Image: https://commons.wikimedia.org (domaine public) L'homme qui a prouvé que des nombres irrationnels existaient a été assassiné pour cela. Il s'appelait Hippasus de Metapontum, et cela s'est passé vers 520 av. Pythagore et de nombreux mathématiciens grecs de l'époque croyaient que tous les nombres étaient entiers ou entiers. C'était quand Pythagore faisait ses fameux calculs de triangle (théorème de Pythagore) qu'il a trébuché sur la racine carrée de deux. Pour faire une histoire courte, il aurait essayé de garder son secret et de l'avoir découvert quand Hippasus l'a publié.
Numéros de Munchausen
 Source: zach.se
Source: zach.se En dehors de faire des suppositions sur 0 ^ 0, 3435 est le seul nombre en plus de 1 où vous pouvez diviser chaque chiffre, le soulever à sa propre puissance, additionner le tout et obtenir le même nombre. Fondamentalement, 3 ^ 3 + 4 ^ 4 + 3 ^ 3 + 5 ^ 5 = 3435 Note: 438579088 fonctionne aussi si vous supposez que 0 ^ 0 = 0. On les appelle les nombres de Munchausen.
La représentation décimale des 7èmes
 Image: https://pixabay.com (domaine public)
Image: https://pixabay.com (domaine public) Les représentations décimales des 7èmes sont le même ensemble de nombres répétés sauf toujours à partir d'un point différent. 1/7 = 0, 142857142857 ... et 2/7 = 0, 285714285714 ... et 3/7 = 0, 428571428571 ...
Comptage binaire des doigts
 Source: mathisfun.com, Image: https://pixabay.com (domaine public)
Source: mathisfun.com, Image: https://pixabay.com (domaine public) Si vous utilisez un binaire, vous pouvez compter jusqu'à 1023 sur vos doigts.
dix!
 Source: reddit.com
Source: reddit.com Il y en a exactement 10! secondes en 6 semaines. Il est plus facile de voir ceci quand vous le divisez en tant que tel: 6 * 7 * 24 * 60 * 60 = 6 * 7 * (8 * 3) * (3 * 2 * 10) * (1 * 3 * 4 * 5) = 6 * 7 * 8 * 9 * 2 * 10 * 1 * 3 * 4 * 5 = 10!
Le numéro de Graham
 Source: ibmathresources.com, Image: https://pixabay.com (domaine public)
Source: ibmathresources.com, Image: https://pixabay.com (domaine public) Le nombre de Graham est si grand que si vous écriviez chaque chiffre aussi petit que possible, il prendrait encore plus de place que dans l'univers observable. En fait, si vous pouviez tenir tous les chiffres dans votre tête, votre cerveau s'effondrerait dans un trou noir (en raison de la densité astronomique des connexions neuronales dont vous auriez besoin).
Répétition des nombres décimaux
 Image: https://pixabay.com (domaine public)
Image: https://pixabay.com (domaine public) Tout décimal répétitif peut être écrit comme une fraction sur un nombre équivalent de 9 (comme la partie répétitive). Par exemple, .456456456 ... serait 456/999
Cartes de brassage
 Source: qi.com, Image: https://www.pexels.com (domaine public)
Source: qi.com, Image: https://www.pexels.com (domaine public) Chaque fois que vous mélangez un paquet de 52 cartes au hasard, vous les avez presque certainement arrangées dans un ordre complètement unique. Ce que nous voulons dire par là, c'est que dans toute l'histoire de l'humanité, personne n'a jamais mélangé un jeu de la même manière. Comment? Eh bien, il y en a 52! façons que vous pouvez commander le pont (52 * 51 * 50 ...) Cela conduit à 8.0658 x 10 ^ 67 possibilités. En comparaison, l'univers n'a que 1 x 10 ^ 18 secondes. Même si tu remuais un paquet toutes les secondes depuis le big bang ... tu serais encore misérablement à court.
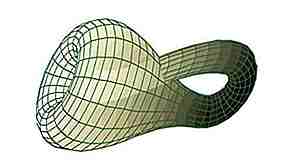
La bouteille de Klein
 Source: math.union.edu
Source: math.union.edu Si vous prenez deux bandes Möbius et que vous étendez les bords pour qu'ils se connectent (en les collant ensemble), vous créez une bouteille Klein. Cette "bouteille" est un exemple de surface non orientable. Fondamentalement, il existe seulement dans 4 dimensions, mais peut être représenté vaguement en 3. Comme la bande de Möbius, il a seulement 1 surface, mais pas d'arêtes. C'est plutôt trippy.
Le théorème frivole de l'arithmétique
 Source: mathworld.wolfram.com, Image: https://pixabay.com (domaine public)
Source: mathworld.wolfram.com, Image: https://pixabay.com (domaine public) Le Théorème frivole de l'Arithmétique indique que, du fait de leur infinité, la grande majorité des nombres naturels sont très, très grands.
Qu'est-ce qui se situe entre 0 et 1

Il y a une quantité infinie de nombres entre 0 et 1 (et 1 et 2, etc.). Par exemple, ½, ⅓, ¼, et vous pouvez continuer à avancer.
Numéros non-calculables
 Source: igoro.com, Image: http://www.pixnio.com (domaine public)
Source: igoro.com, Image: http://www.pixnio.com (domaine public) Presque tous les nombres réels sont irrationnels. Encore plus, la plupart des nombres irrationnels ne sont même pas calculables. Et pour vraiment boggle votre esprit, chaque nombre que vous avez jamais vu dans votre vie est calculable, y compris des nombres infiniment répétitifs comme pi (parce que vous pouvez créer un algorithme pour le calculer). Donc, pour simplifier les choses, il y a une quantité infinie de chiffres que nous ne verrons jamais (en fait ... la plupart d'entre eux) parce que nous n'avons aucun moyen de calculer ces chiffres. En un sens, ils sont la «matière noire» des mathématiques. Nous savons qu'ils sont là et qu'ils constituent la majorité indicible des nombres, mais nous n'avons aucun moyen de les atteindre. Note: La constante de Chaitin est un exemple de nombre non-calculable, mais malheureusement ... ce n'est pas calculable.
Les différents types d'infini
 Source: math.brown.edu, Image: https://pixabay.com (domaine public)
Source: math.brown.edu, Image: https://pixabay.com (domaine public) Bien que les entiers soient infinis, il y a infiniment plus de nombres réels que d'entiers. Comment cela peut-il être si les entiers sont déjà infinis? C'est parce qu'il y a deux types d'infini ... dénombrables et indénombrables. Les entiers sont infiniment dénombrables, alors que les nombres réels ne le sont pas (parce qu'ils incluent aussi les nombres irrationnels). Donc, cela conduit à des conclusions fous. Le nombre d'entiers positifs (0, 1, 2, ...) est exactement le même que le nombre d'entiers positifs et négatifs combinés (..., -3, -2, -1, 0, 1, 2, 3, ...). Bien que ces deux ensembles infinis soient égaux, ils sont tous deux plus petits que l'ensemble infini de nombres réels. En fait, il y a infiniment plus de nombres entre deux entiers aléatoires (0 et 1 par exemple) que dans l'ensemble infini des entiers!
Les nombres normaux
 Source: mathworld.wolfram.com
Source: mathworld.wolfram.com Un nombre normal est fondamentalement un nombre irrationnel qui n'a pas plus d'un chiffre donné qu'un autre. Ainsi, par exemple, dans le numéro 4.56856948576434 ... chaque chiffre doit apparaître à peu près le même nombre de fois jusqu'à l'infini. Bien qu'il y ait une preuve approximative pour montrer que la plupart des nombres réels sont normaux, et que nous soupçonnons que des nombres comme pi et e sont normaux, nous n'avons toujours pas été capables de le montrer.
Les nombres transcendantaux
 Source: mathworld.wolfram.com
Source: mathworld.wolfram.com Bien que presque chaque nombre réel et complexe soit transcendantal (par opposition à algébrique, qui est fondamentalement n'importe quel nombre qui est la racine d'un polynôme), il y en a seulement quelques-uns qui sont connus, principalement parce qu'il est vraiment difficile de prouver qu'un nombre est transcendantal. Les nombres transcendants les plus connus sont e et pi.
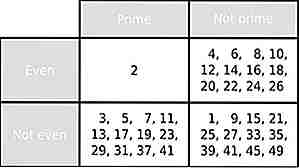
Le premier prime solitaire
 Source: mathworld.wolfram.com, Image: https://commons.wikimedia.org (domaine public)
Source: mathworld.wolfram.com, Image: https://commons.wikimedia.org (domaine public) Chaque nombre premier jusqu'à l'infini est impair. Sauf pour 2.
L'effet de l'infini sur la probabilité
 Image: https://pixabay.com (domaine public)
Image: https://pixabay.com (domaine public) Le concept de l'infini a des effets fous sur la probabilité. Si vous deviez choisir aléatoirement un nombre réel, la probabilité qu'il soit rationnel (1, 2, ¾, 78/56, ...) est 0. Cela revient au fait que les nombres irrationnels sont infiniment infinis, alors que les nombres rationnels sont dénombrables infinis. Et, l'infini dénombrable sur l'infini indénombrable est 0.
999 ... = 1
 Image: https://commons.wikimedia.org (domaine public)
Image: https://commons.wikimedia.org (domaine public) .999 ... est égal à 1. Par ce point, votre esprit est probablement tellement bogué avec le concept de l'infini que vous accepterez probablement tout ce que nous vous disons, mais nous le prouverons. Vous savez que .333 ... est égal à ⅓ et .666 ... est égal à ⅔. ⅓ + ⅔ = 1 et .333 ... + .666 ... = .999 .... Une autre façon d'y penser est que si .999 ... n'est pas égal à 1, il devrait y avoir un certain nombre entre .999 ... et 1. Ce qui, grâce au concept de l'infini, ne l'est pas.
La fonction Dirichlet
 Source: mathworld.wolfram.com
Source: mathworld.wolfram.com Selon la fonction de Dirichlet, entre deux nombres irrationnels, il y a un nombre rationnel. La partie folle? Il y a infiniment plus de nombres irrationnels que de nombres rationnels (comme nous l'avons précédemment établi). Alors ... comment tous les deux nombres irrationnels peuvent-ils avoir un nombre rationnel entre eux? Vous vous attendriez à manquer de nombres rationnels. Mais l'infini ne se comporte pas comme nous le souhaitons.
L'identité d'Euler
 Source: mathworld.wolfram.com
Source: mathworld.wolfram.com L'identité d'Euler est souvent citée comme un exemple de beauté mathématique. C'est e ^ (pi * i) + 1 = 0. Il contient 5 des constantes mathématiques les plus fondamentales 0, 1, e, pi et i. En outre, trois des opérations arithmétiques de base se produisent exactement une fois: l'addition, la multiplication et l'exponentiation. Benjamin Peirce, un mathématicien noté a dit une fois après l'avoir prouvé dans une conférence, "l'identité est absolument paradoxale; nous ne pouvons pas le comprendre, et nous ne savons pas ce que cela signifie, mais nous l'avons prouvé, et nous savons donc que cela doit être la vérité. "
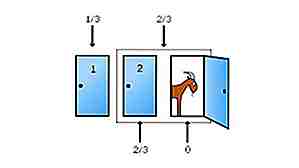
Le problème de Monty Hall
 Source: mathworld.wolfram.com, Image: https://commons.wikimedia.org (domaine public)
Source: mathworld.wolfram.com, Image: https://commons.wikimedia.org (domaine public) Le problème de Monty Hall est un exemple célèbre de la façon dont la probabilité peut être contre-intuitive. Disons que sur un jeu télévisé il y a trois portes. Derrière l'une d'entre elles se trouve une voiture tandis que les deux autres cachent des chèvres. Vous choisissez d'ouvrir la porte 1. L'hôte, cependant, sait ce qu'il y a derrière les portes. Il ouvre la porte 3 pour révéler une chèvre. Maintenant, il vous demande si vous souhaitez changer votre choix à la porte 2. Que faites-vous? La réponse est que vous devriez changer votre choix. Pourquoi? Parce qu'en changeant à la porte 2 vous avez une chance de gagner la voiture tout en restant sur la porte 1 vous avez une chance approximative. La meilleure façon de visualiser cette solution contre-intuitive est d'augmenter le nombre de portes. Disons maintenant qu'il y a 100 portes. Vous choisissez la porte 37. L'hôte ouvre maintenant toutes les portes pour révéler les chèvres, sauf pour la porte 83. Voulez-vous changer votre choix de 37 à 83? Ou resteriez-vous le 37? Le fait est que vos chances de gagner la voiture augmenteront considérablement en passant à la porte 83.
La différence entre 1 million et 1 milliard

Un million de secondes représente environ 11 jours et demi. Un milliard de secondes est juste un peu moins de 32 ans.
Le principe du pigeonnier
 Source: mathworld.wolfram.com, Image: https://commons.wikimedia.org (domaine public)
Source: mathworld.wolfram.com, Image: https://commons.wikimedia.org (domaine public) Si vous avez 2 types de chaussettes dans votre tiroir et que vous en prenez aléatoirement 3 sans regarder, vous êtes assuré d'avoir une paire assortie. Alors que pour certaines personnes c'est évident, pour d'autres cela peut être plus difficile à saisir. Il est basé sur quelque chose appelé le principe du pigeonnier. Fondamentalement, si vous avez n types de quelque chose, alors vous devez choisir aléatoirement n + 1 de cette chose afin d'obtenir une correspondance. Donc, si vous avez 5 types de chaussettes différentes dans votre tiroir et que vous en saisissez aléatoirement 6 ... vous êtes assuré d'avoir une correspondance. Cela peut être génial pour s'habiller dans l'obscurité!
La somme de tous les entiers positifs de 1 à l'infini
 Source: voir ci-dessous, Image: https://commons.wikimedia.org (domaine public)
Source: voir ci-dessous, Image: https://commons.wikimedia.org (domaine public) Maintenant, préparez-vous pour la chose la plus époustouflante que vous n'entendrez jamais dans votre vie. Si vous additionnez tous les entiers positifs de 1 à l'infini ... qu'est-ce que vous obtenez? Avez-vous deviné -1/12? Parce que c'est la bonne réponse. Nous savons. Cela semble absolument ridicule et dans une certaine mesure il est. Pourquoi? Parce que tout ajouter jusqu'à l'infini est impossible et sûr de donner des résultats ridicules. Pour rendre les choses encore plus folles pour vous, ce résultat est en fait très bien connu en physique, en particulier la théorie des cordes. En fait, si vous ne pouvez toujours pas y croire, nous vous suggérons de regarder cette vidéo réalisée par les physiciens Tony Padilla et Ed Copeland de l'Université de Nottingham. Ils expliquent la folie mieux que nous pouvons - https://www.youtube.com/watch?v=w-I6XTVZXww.
Note: le résultat provient en grande partie du fait que l'infini défie nos attentes. L'infini n'est pas un nombre, c'est un concept. Des choses comme l'addition et la soustraction ne fonctionnent pas de la même façon quand vous impliquez l'infini (comme la physique ne fonctionne pas de la même manière quand vous êtes au milieu d'un trou noir).
Plus d'informations: il vaut également la peine de se pencher sur la sommation de Ramanujan et la série de Grandi:
https://en.wikipedia.org/wiki/Ramanujan_summation
https://en.wikipedia.org/wiki/Grandi's_series
Une autre ressource:
http://www.bradyharanblog.com/blog/2015/1/11/this-blog-probably-wont-help
Photos: Image vedette: https://commons.wikimedia.org (domaine public), 20. pixel max, 16. Tttrung, bouteille Klein2, CC BY-SA 4.0, 11. Mehran Moghtadaei, PP 1280 × 1024, CC BY- SA 3.0, 10. Stephen J. Brooks (discussion), Algebraicszoom, CC BY 3.0, 6. Judy Breck via flickr, CC BY-SA 2.0, 5. Quinn Dombrowski de Chicago, États-Unis, Identity Graffito d'Euler, CC BY-SA 2.0, 3. Cmglee, Visualisation 1 milliard, CC BY-SA 3.0,




